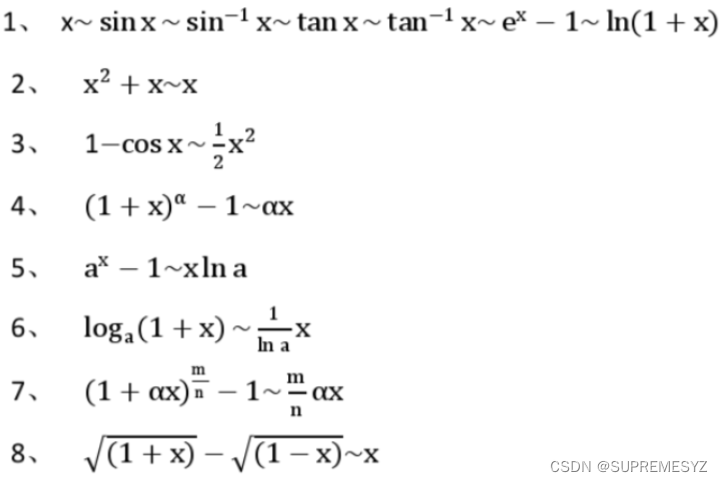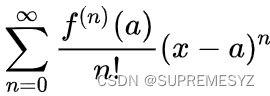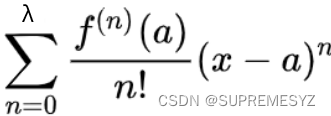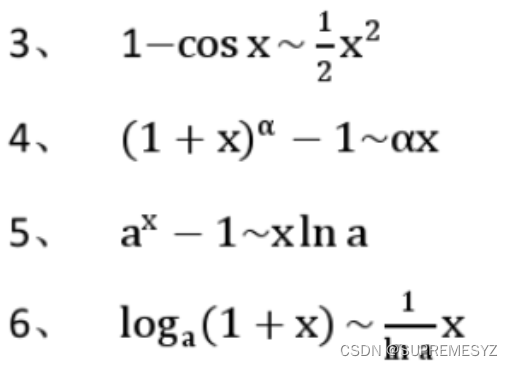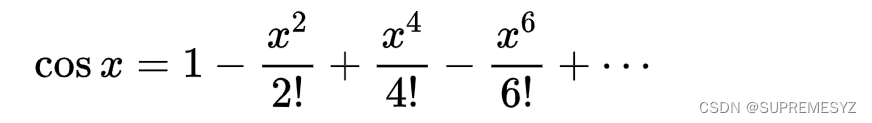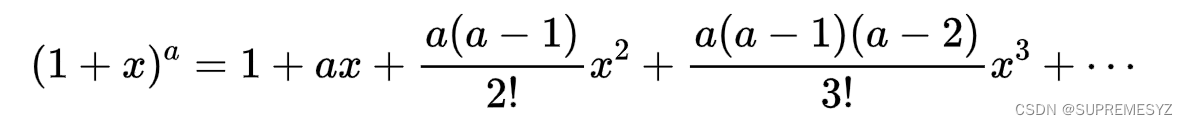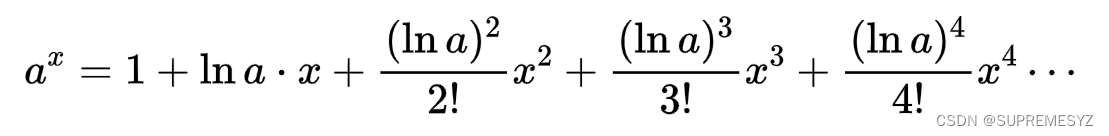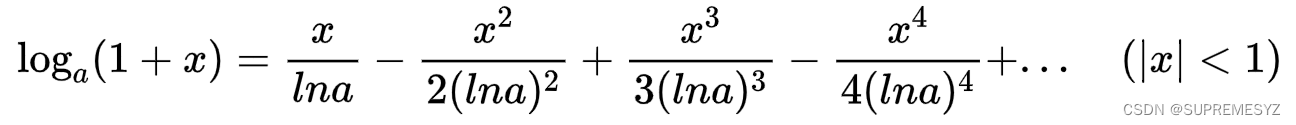等价无穷小（以及和泰勒级数的关系）

emmm

一般所说的等价无穷小

特指x→0时可以互相拿来替换的函数

大概就是下面这一坨

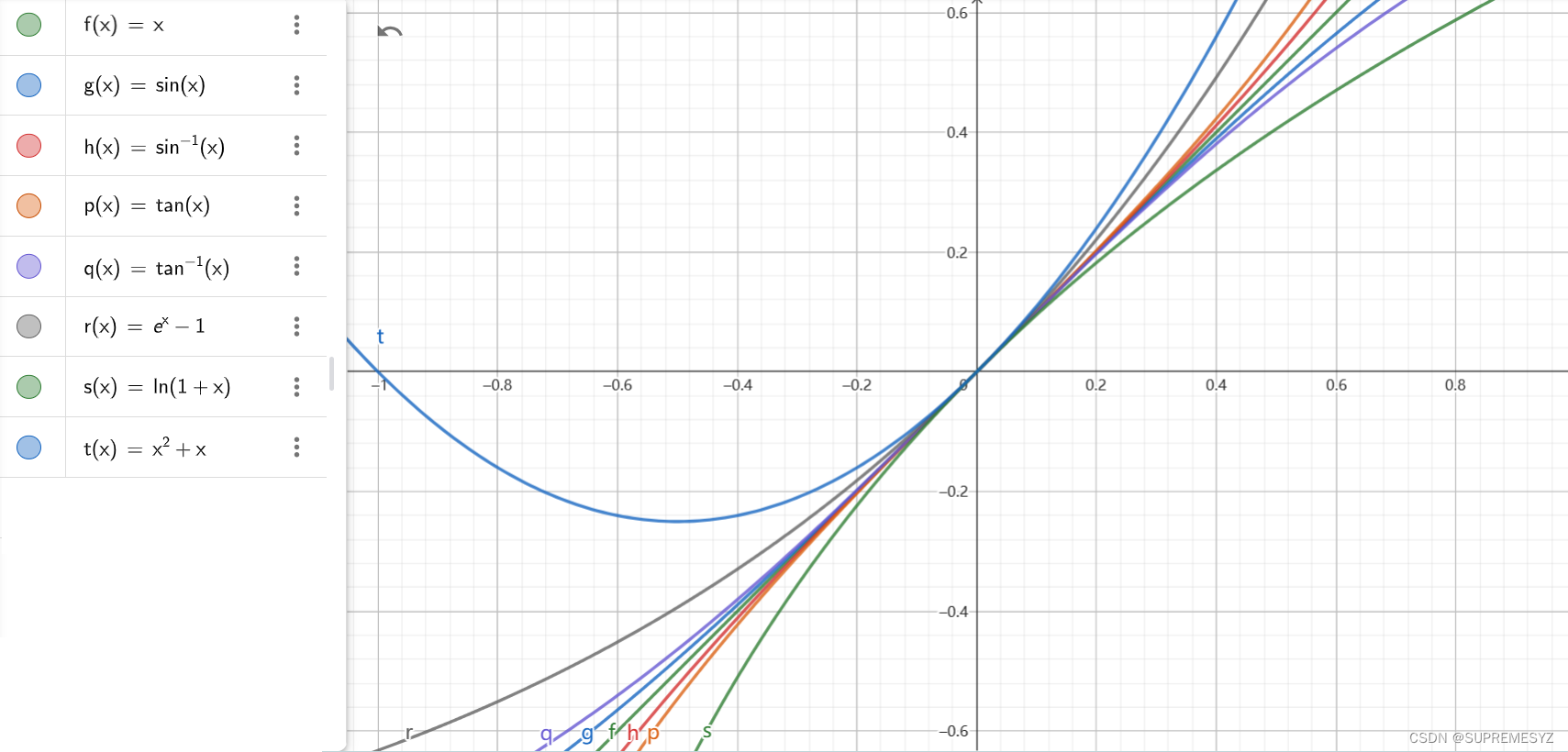
看起来还算比较友好，对吧？

这就引出了下面的问题

可以很容易看出

在x=0附近，这些函数曲线几乎重合

为什么会这样？

要继续探讨，就不得不提到泰勒级数

就是下面这一坨

泰勒级数的作用是在某一点使用多项式对某一函数近似拟合

原理：

就是保证多项式的每一阶导数都等于原函数（包括零阶，也就是零点的函数值）

为什么还有个阶乘？

因为幂级数求导本身自带 “buff” 加成

比如求 x^10 的10阶导数

结果刚好是10的阶乘

除以阶乘就是为了抵消幂级数自带的 “buff” 影响

其实还有个东西叫做泰勒多项式

就是把上面的 ∞ 换成一个具体的数，比如λ

可以把泰勒级数看作泰勒多项式的极限状态（趋于无穷嘛）

有一点像积分与求和的关系......

说了半天，泰勒级数和等价无穷小有啥关系

可以这么说，等价无穷小就是“阉割版”的泰勒级数，是泰勒级数的“低精度版本”

举个例子：

现在要你用 x^2 构造函数，使其在x=0处能够近似代替y=x，应该怎么做？

想想泰勒级数

用一个函数拟合另一个函数（在某一点附近）

其实就是让二者的各阶导数相同（相同的阶数越多，拟合程度越好）

因为不需要特别高的精度

我们只取0阶（就是该点函数值）和1阶导数

首先(x^2)在x=0处的值就是零，y=x在x=0处的值也是零，不用管

而一阶导数 (x^2) ' = 2x，代入0得0，与y=x导数为1不同

怎么办？加一个x不就好了，这样 (x^2+x) '=2x+1，代入0得1

结果就是在x=0附近，可以用 y=x^2+x 近似代替y=x

至于其他的像 e^x-1，ln(1+x)等等，都是一个思路

也可以理解为拿这个函数去往y=x上贴，让y=x成为这个函数的切线

而像sinx，arcsinx，tanx，arctanx

他们本身就满足0阶和1阶导分别等于0和1（在x=0处）

也就是y=x刚好是他们在0处的切线，根本就不需要动

上面这些算是“逆向”泰勒变换，用已有函数去逆向近似y=x这个多项式（其实它有2项，常数项是0 看不出，实际应该是y=0+x）

反过来你会发现，它们的泰勒展开式前两项刚好就是y=0+x，即y=x

还有一些直接正向泰勒展开再整理的，比如：

就是下面的式子取前两项再整理（这与我们取0阶和1阶导精度一致）

说来说去，最后其实就是泰勒级数